티스토리 뷰
논문 제목 : Densely Connected Convolutional Networks
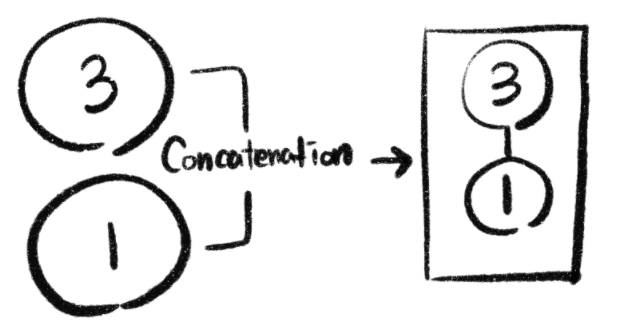
오늘은 Densely Connected Convolutional Networks에서 소개한 DenseNet에 대해 다뤄보려 한다. DensNet은 이전에 다루었던 ResNet의 Shortcut 개념을 더 확장하여 CNN 구조를 바꾸는 시도를 하였는데, 바로 입력값의 Summation에서 Concatenation으로의 변화이다.

Summation을 '덧셈'으로 해석할 수 있다면, Concatenation은 '결합'으로 해석할 수 있다. 수치적으로 무언가를 결합한다는 의미가 아니라, 말 그대로 입력값들을 사슬처럼 이어 결합 (연결) 하는 것을 의미한다. 그럼 입력값들을 합하지 않고, 결합함으로써 어떤 효과가 있었는지 한번 알아보자!

1. Abstract

초록에서는 Shortcut connection을 소개하며, DenseNet에서는 이를 어떻게 적용했는지 간략히 설명하고 있다.
최근 CNN에 대한 많은 연구결과로부터 layer 간에 shortcut connection을 구성하면 convolution network가 상당히 깊어질 수 있고, 더 정확해지며, 학습시키는데 매우 효율적이라는 것이 입증되었다. 하지만, 기존의 covolution netwokr는 ResNet에서 볼 수 있듯이 바로 그다음 레이어에만 connection을 연결하기에 L개의 layer가 L개의 connection만 가질 수 있었는데, DenseNet에서는 각 layer가 다른 모든 layer에 연결되기에 $ \frac{L(L + 1)}{2} $ 개의 연결을 가질 수 있다고 한다.
2. Introduction

소개에서는 DenseNet의 Shortcut connection 개념인 Dense Connection을 ResNet의 Shortcut Connection과 비교하며 이에 대해 더 자세히 설명한다.
CNN의 깊이가 상당히 깊어지면서 새로운 문제가 생겼다. 이전에 ResNet을 다룰 때에도 언급했었는데, 바로 많은 layer를 거치는 입력값 또는 기울기에 대한 정보가 네트워크의 끝단(순전파) 또는 시작점(역전파)에 도달할 때 대부분 사라진다는 것이다. 이를 해결하기 위해 ResNet과 Highway Networks는 identity connection을 통해 신호를 우회하는 것을 시도하였다. 이때 두 모델은 네트워크 구조 및 학습 절차와 같은 접근법이 서로 달랐지만, 이전의 layer에서 다음 layer로 바로 연결되는 short path를 만든다는 점은 같았다.
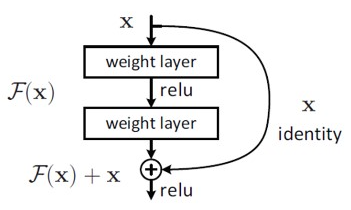

이 논문에서는 이러한 connection에서 영감을 받았는데, layer 간 정보 흐름을 최대화하기 위해 모든 layer들이 서로 연결되게끔 구성하였다. 각각의 layer는 이전 layer 1개뿐만 아니라, 이전의 모든 layer들로부터 추가적인 정보를 얻고, 그들 고유의 feature map을 그다음의 모든 layer로 전달한다.
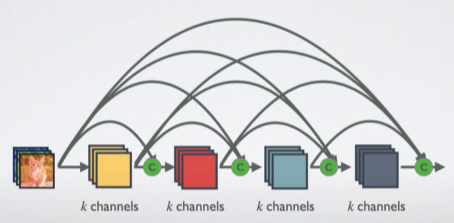
이때, ResNet과는 달리 feature들을 Summation 하지 않고, 이들을 Concatenating 하여 l 번째 layer가 이전의 모든 conv block들의 feature map들로 구성된 l 개의 input을 갖게끔 하였다. 이렇게 desne 하게 연결되었다는 이유로 이 구조를 DenseNet이라 부른다.

DenseNet은 기존의 convolution network에 비해 장황한 feature map에 대한 불필요한 학습이 필요 없다. 왜냐면 이제는 이전의 모든 layer로부터 정보를 받기에, feature map이 더 견고해지기 때문이다. 따라서 더 적은 파라미터 수를 요구한다.
ResNet은 추가적인 identity transformation을 통해 정보를 보존한다. 하지만, 대부분의 layer들은 적게 기여하고, 결국 학습 과정에서 이러한 정보들이 random 하게 drop 될 수 있다. 이는 ResNet이 정보를 순환하게끔 해주지만, 각각의 layer가 weight을 가지기에 파라미터 수가 상당히 큰 편이다.
반면에, DenseNet은 네트워크에 더해지는 정보를 명확하게 구분하면서 정보를 보존한다. DenseNet은 매우 narrow 한데, feature map을 그대로 보존하면서 feature map의 작은 집합을 네트워크 전역에서 관리하는 뭉쳐있는 정보 덩어리에 추가하기 때문이다.

게다가, 정보와 기울기의 개선된 흐름 덕에 학습하기도 매우 쉽다고 한다. 각각의 layer들은 loss function 및 input signal로부터의 기울기에 직접적으로 접근할 수 있기에 네트워크의 구조가 깊더라도 학습이 쉬워진다. 추가로, dense connection은 regularizing 효과가 있어 오버 피팅을 줄여준다고 한다.
3. Related Work

Related Work에서는 DenseNet과 이에 영향을 준 이전의 다른 네트워크 모델을 비교 분석하고 있다.
여러 해를 거듭하며 CNN 모델이 발전해왔고, 그중 Highway Network는 100-layer가 넘는 end-to-end 네트워크를 효과적으로 학습시킬 수 있는 수단을 제공한 첫 번째 구조였다. 이는 우회 경로를 사용함으로써 100개 이상의 layer를 최적화할 수 있었는데, 이러한 deep 네트워크의 학습을 쉽게 하는 데 있어 우회 경로는 이제 당연한 것으로 여겨진다. 이러한 점은 이후에 ResNet이 identity mapping을 우회 경로로 사용함으로써 한번 더 입증하였다.

최근에는 stochastic depth를 적용하여 1202-layer ResNet을 학습시키는 것이 가능해졌는데, 이는 학습 가능한 layer를 random 하게 drop 함으로써 달성할 수 있었다. 즉, deep network에는 어마한 양의 중복성이 있어 모든 layer가 필수인 것은 아님을 의미하는데, DenseNet은 여기서 부분적으로 영향을 받았다고 한다.


네트워크를 깊게 만드는 직교(Orthogonal)적인 접근법은 바로 폭을 키우는 것이다. (여기서 '직교'란 하나의 접근법을 이용해 둘 이상의 문제점을 동시에 해결하는 것이 아니라, 하나의 문제점만 해결한다는 의미.) 그 예로 Inception module을 사용하여 여러 사이즈의 필터(1 x 1, 3 x 3, 5 x 5)로부터 만들어진 feature map들을 concatenate 한 GoogLeNet과, 더 넓은 residual block을 가지는 변형 ResNet, 그리고 FractalNet 등이 있다.
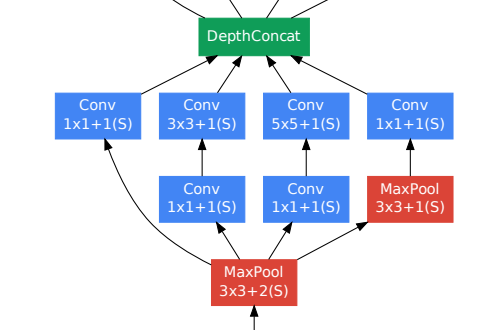
이때, DenseNet은 극도로 deep 하거나 wide 한 구조로부터 representational power를 끌어내는 대신 feature의 재사용을 통해 네트워크의 잠재력을 활용하였다. 그 결과, DenseNet은 학습하기 쉬우면서도 효율적인 parameter를 가진 압축된 모델을 만들 수 있었고, 후속 layer의 input에 variation을 주면서 효율을 개선할 수 있었다. 그리고 이 점이 바로 DenseNet과 ResNet 간의 주요 차이점이며, Inception module보다 더 간단하고 효율적일 수 있는 이유라고 한다.
4. DenseNets

이제 DenseNet의 세부 구조에 대해 뜯어볼 것인데, 먼저 용어에 대해 정리하자면 다음과 같다.
$ x_0 $ : conv network를 통과한 single image
$ H_l(\cdot) $ : $ l $ 번째 layer의 비선형 변환. 이는 BN, ReLU, Pooling, Conv로 구성된 composite function이다.
$ x_l $ : $ l $ 번째 layer의 출력
ResNets

먼저 전통적인 feed-forward 방식과 달리, ResNet은 identity function을 이용해 비선형 변환을 우회하는 skip connection을 추가한다. 즉, 수식이 residual을 더하는 모양이 된다.

이때, ResNet의 장점은 identity function을 통해 gradient가 뒤쪽 layer에서 앞쪽 layer로 직접 흐를 수 있다는 점이다. 하지만, identity function과 $ H_l $ 의 출력이 Summation으로 합해지기에 네트워크의 정보 흐름을 방해할 수도 있다.
Dense Connectivity

앞서 말한 정보 흐름의 방해를 개선하기 위해 DenseNet은 또 다른 connectivity pattern을 선보였다. 이는 바로 모든 layer가 모든 후속 layer로 연결되는 향하는 direct connection을 가지며, 결과적으로 $ l $ 번째 layer는 모든 이전 layer의 feature map인 $ x_0, ..., x_{l - 1} $ 을 입력으로 받는 것이다. 여기서 $ [x_0, ..., x_{l - 1}] $은 $ 0, ..., l - 1 $ 번째 layer에서 생성된 feature map들의 concatenation이다. 이러한 dense connectivity로 인해 이 모델을 DenseNet이라 부른다.
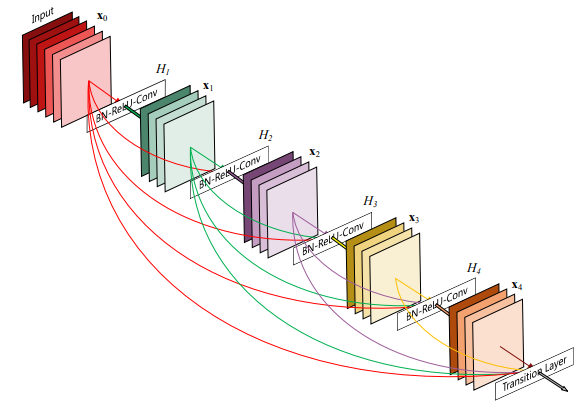
Composite function

$ H_l(\cdot) $ 은 BN $ \rightarrow $ ReLU $ \rightarrow $ 3 x 3 Conv 순서로 구성된 composite function이다.

Pooling layers

Concatenation 연산은 feature map의 크기가 달라질 경우 사용이 불가능하다. 따라서 down-sampling layer를 이용하여 feature map의 크기를 바꾸는데, 이를 위해 네트워크를 여러 개의 dense block으로 나누고, 그 사이에 transition layer를 둔다.
transition layer는 convolution 연산 및 pooling을 수행하는데, 이는 BN layer $ \rightarrow $ 1 x 1 Conv $ \rightarrow $ 2 x 2 Average pooling layer로 구성된다.

Growth rate


$ l $ 번째 layer는 $ k_0 + k(l - 1) $ 개의 input feature map을 가지는데, 여기서 $ k_0 $ 는 input layer의 채널 수이다. DenseNet과 다른 구조의 중요한 차이점은 very narrow layer를 가질 수 있다는 것인데, 여기서 k는 하이퍼 파라미터로 네트워크의 growth rate를 의미한다. 섹션 4에서 상대적으로 작은 k값으로도 충분히 좋은 결과를 얻을 수 있다는 것을 확인할 수 있는데, 이는 각 layer들이 block내에 있는 모든 이전 feature map에 접근하여 collective knowledge에 접근할 수 있음을 의미한다.
여기서 feature map을 네트워크의 전역 state로 볼 수 있으며, 각 layer들은 이 전역 state에 k개의 feature map을 추가하는 것이라고 보면 된다. 이때, growth rate는 전역 상태에 각 layer가 기여하는 새로운 정보의 양을 조절한다. 이렇게 한번 추가된 global state는 어디에서나 접근할 수 있기에 layer 간에 복제할 필요가 없다.
Bottleneck layers

이전의 연구 결과로 bottle neck구조를 통해 input feature map을 줄일 수 있다는 것이 확인되었는데, DenseNet에서는 이 bottleneck 구조가 특히 효과적이어서 $ H(l) $ 을 BN $ \rightarrow $ ReLU $ \rightarrow $ Conv (1 x 1) $ \rightarrow $ BN $ \rightarrow $ ReLU $ \rightarrow $ Conv (3 x 3)로 구성하였고, 이를 DenseNet-B라 부르기로 하였다. 실험에서는 각각의 1 x 1 conv가 4k feature map을 생성하게끔 하였다.

Compression

Transition layer를 통해 feature map의 수를 줄일 수 있다고 앞서 말하였는데, 만약 dense block이 m개의 feature map을 가지는 경우 transition layer는 $ \llcorner \theta_m \lrcorner $ 개의 feature map으로 줄여준다. 이때 $ \theta $ 는 $ 0 < \theta \le $ 1로, 이를 copression factor라 한다. 만약 $ \theta = 1 $ 이면, feature map의 수는 바뀌지 않는다. $ \theta < 1 $ 이 적용된 DenseNet을 DenseNet-C라 하고, 실험에서는 $ \theta = 0.5 $ 를 사용하였다. 이때 bottleneck 및 $ \theta < 1 $ 이 모두 적용된 모델을 DenseNet-BC라 부른다.
Implementation Details

ImageNet을 제외한 나머지 데이터셋에 대한 실험에서 사용한 DenseNet은 모두 같은 layer 수로 구성된 3개의 dense block을 가진다.
첫 번째 dense block에 들어가기 전에 16개의 feature map을 출력하는 convolution이 수행되며, 이때 커널 사이즈는 3 x 3이다. 여기서 feature map의 사이즈를 고정시키기 위해 1 pixel 크기의 zero padding을 수행한다. 추가로 dense block 사이에 1 x 1 conv $ \rightarrow $ 2 x 2 average pooling layer로 구성되는 transition layer가 있으며, 끝단에는 GAP 및 softmax layer가 위치한다. 3개의 dense block의 사이즈는 각각 32 x 32, 16 x 16, 8 x 8이며, basic DeseNet과 DenseNet-BC는 각각 다음 configuration을 사용하였다.
basic DenseNet
{L = 40, k = 12}
{L = 100, k = 12}
{L = 100, k = 24}
DenseNet-BC
{L = 100, k = 12}
{L = 250, k = 24}
{L = 190, k = 40}

ImageNet을 대상으로 한 실험에서는 DenseNet-BC를 사용했으며, 이때 input image는 224 x 224이고, 4개의 dense block으로 구성된다. 자세한 구조는 다음 표를 참고하면 알 수 있다.
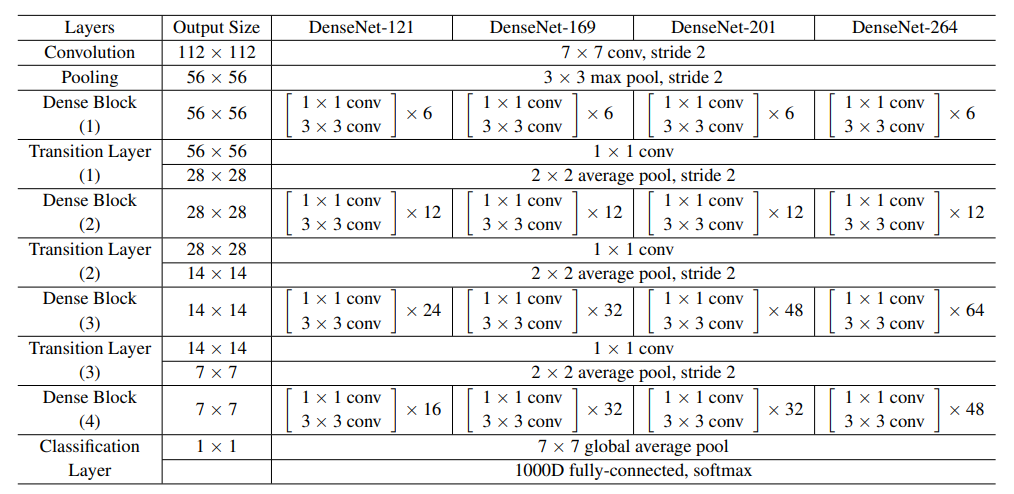
5. Experiments
실험 섹션에서는 학습한 데이터셋의 종류, 학습 방법, 각 데이터셋에서의 결과에 대해 설명하고 있다.
Dataset
CIFAR, SVHN, ImageNet 사용하였으며, 데이터 셋의 특징에 따라 데이터 전처리를 다르게 적용
Training
CIFAR와 SVHN은 Batch 사이즈를 64로 하고, 각각 300 / 40회의 epoch을 거쳐 학습 진행
ImageNet은 Batch 사이즈를 256으로 하고, 90회의 epoch을 거쳐 다양한 depth L과 growth k에 대해 학습을 진행하였다. 자세한 내용은 아래 표를 참고하면 알 수 있다.
Classification Results
기존 모델에 비해 성능이 좋았다는 내용들이어서 특별히 다룰만한 내용은 따로 없다.
CIFAR와 SVHN에 대해서는 Accuracy, Capacity, Parameter Efficiency, Overfitting 관점에서 모두 좋은 성능을 보였고,

ImageNet에 대해서는 비슷한 성능을 보였지만, 파라미터 수가 현저히 적었다고 한다.

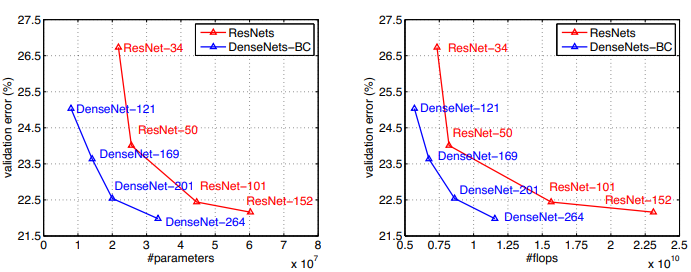
6. Discussion
이 섹션에서도 기존 모델에 비해 성능이 좋았다는 내용들이며, 특별히 다룰만한 내용은 없다.
DenseNet과 ResNet은 서로 매우 유사하지만, DenseNet의 경우 입력을 concatenation 한다는 점에서 다르다. 따라서 모든 DenseNet layer에서 학습된 feature map을 모든 후속 layer에 연결할 수 있다는 것이다.
DenseNet은 Model compactness, Feature Reuse 면에서 탁월하였고, 수많은 shortcut connection이 마치 deep supervision처럼 동작하여 중간 layer들이 discriminative 한 특징을 배우도록 강제하는 효과가 있었다고 한다. 또한 stochastic depth가 적용된 reisidual network와 그 방식은 매우 다르지만, stochastic depth에 대한 DenseNet만의 해석이 regularizing 효과를 성공적으로 만들어낼 수 있었다고 한다.
다양한 모델 중, DenseNet-BC가 가장 좋은 성능을 보였으며, 이 모델이 ResNet과 비슷한 성능을 내는 데까지 필요한 파라미터는 겨우 1/3에 불과하였다고 한다.
7. Conclusion

결과적으로, DenseNet은 degradation이나 overfitting 없이 정확도를 꾸준히 개선할 수 있었으며, 상당히 적은 수의 파라미터 및 연산량으로도 최고 수준의 성능을 낼 수 있었다.
이는 DenseNet이 identity mapping, deep supervision, diversified depth를 통합하여 네트워크 전역에서의 feature reuse를 가능케 하였고, 그 덕에 더 작으면서도 정확한 모델을 학습할 수 있었기 때문이다.
참고 문헌
2. velog.io/@dyckjs30/DenseNet
'방구석 논문 리뷰' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 그래프
- mmc_spi
- 알고리즘
- 너비우선탐색
- SQL 완주반
- ResNet
- 구글 머신러닝 부트캠프
- ARM Cortex-M3 시스템 프로그래밍 완전정복1
- 코딩테스트
- ARM 역사
- 패스트캠퍼스
- CNN
- 깊이우선탐색
- spidev
- 머신러닝
- TensorFlow Developer Certificate
- Shortcut
- 딥러닝
- Cortex-M0
- Cortex-M3
- DFS
- 강의제안
- 그래프탐색
- BFS
- 머신러닝 엔지니어
- 완주반
- 텐서플로우 자격증
- 딥러닝 엔지니어
- 백준
- Cortex 시리즈
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
